Hammer of Math: Infinity Face Off Rolls

This week’s Hammer of Math looks at the math behind rolls in Infinity, a very popular (and fun) sci-fi skirmish game from Corvus Belli.

While Games Workshop continues to be the juggernaut of tabletop miniature wargames, several other companies make high quality products that are just as fun. One such example is Infinity, a skirmish sci-fi game that Corvus Belli has produced since 2005. Currently using the N4 rules set (which are available for free on their website), Infinity is a dynamic and fast-paced game with a huge amount of depth and complexity. The core mechanic of the game are d20 rolls that are used to determine the success of an event. There are two types of roll; Normal Rolls and Face to Face Rolls.

Normal Rolls

A Normal Roll in Infinity is a fairly simple concept; you roll a d20 and compare it to the Success Value (SV). The SV is equal to the relevant Attribute plus any Modifiers (MODs). If the result is less than the SV then the roll is a success. If the result equals the SV then it’s a critical success. Otherwise it’s a failure.

The total value of the modifiers applied to a particular roll can never be less than -12 or more than 12. If the resulting SV is less than 1 then the roll automatically fails. If the SV is greater than 20 than SV is considered to be 20 and the player adds the amount by which the SV exceeded 20 to the result (so a SV of 23 would add 3 to the result). This increases the chance of obtaining a Critical result. 

Face to Face Rolls

One of the major differences between games like Warhammer 40k and Infinity is that a significant number of rolls are contested in what’s known as Face to Face Rolls. This means that both players are engaged at nearly every stage of the game. In a Face to Face Roll the two players roll off and then compare the results using the following process:

1. Any failures are discarded; if all of the rolls are failures then the Trooper does not achieve their goal.
2. A Trooper who achieves one (or more) Critical Roll cancels all of the enemy successes; if both Troopers achieve one (or more) Critical Rolls then no effects are applied. The enemy roll will cancel any values which are less than it.
3. If neither Trooper achieved a Critical Roll then the highest successful roll is compared; if the rolls are the same then the rolls cancel each other and no effects are applied.
4. If there is no tie then the Trooper with the highest successful roll succeeds, and any results that are equal to or greater than the highest roll of the enemy are applied. Note that even if a particular roll is tied with the highest roll of the enemy it still counts as a success if the Trooper has another successful roll that’s higher. The rule regarding ties cancelling everything only occurs if the tie is between the highest roll of each Trooper.

This is a very, very deep system which offers a massive amount of potential and variation. It’s a difficult challenge, not only in terms of establishing the probabilities but also in terms of determining how to present the results. For this article I decided to focus on a relatively simple question; what is the probability of success given an attacker and defender’s relative success value for a different range of dice rolls? In this case success is defined by any effects applied to the target, and does not calculate the number of successes nor the probability of the defender getting their own success. To accomplish this I put together a Monte Carlos method in Python, running one million iterations for each combination of Attacker and Defender SV. Eventually we might be able to convert this into an online calculator, but for now it’s making pretty charts.

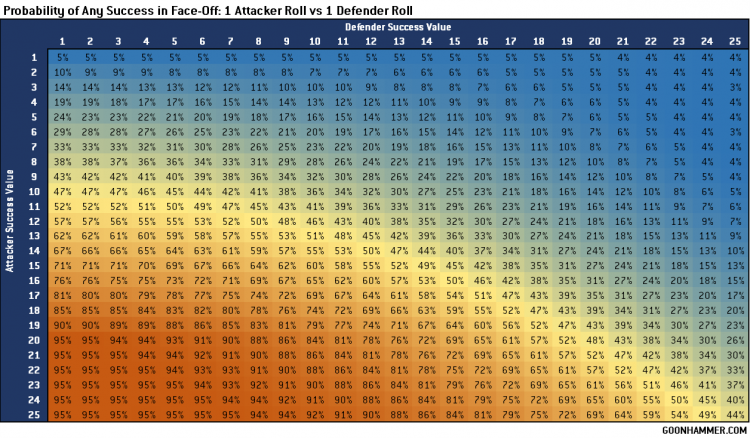
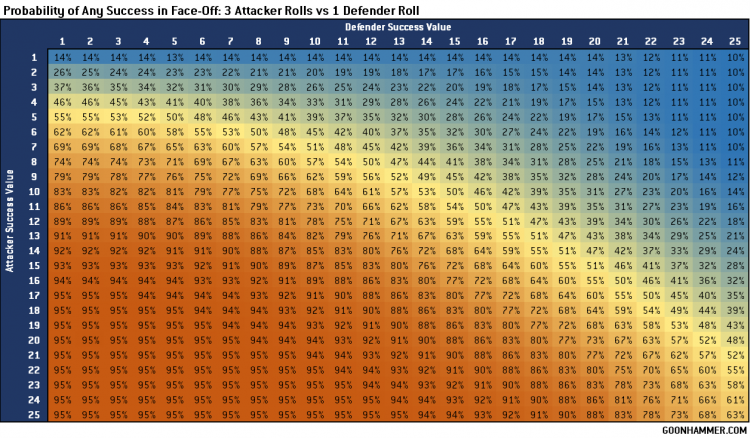
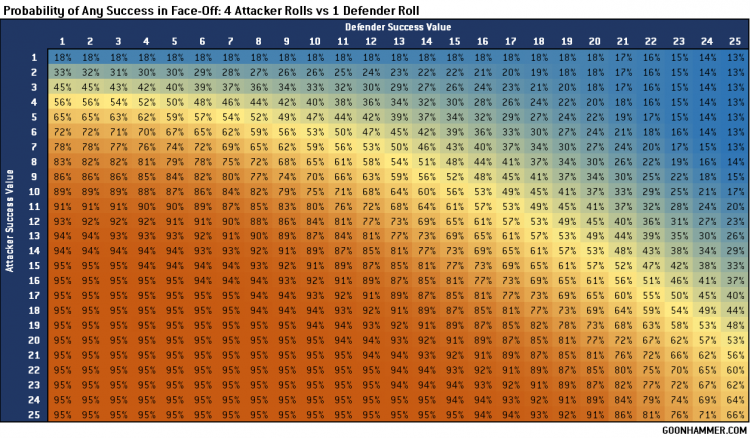
The charts above show the probability of getting any successes based on the number of attacks and the relative SVs for the Attacker and Defender. It’s interesting to note that success is never guaranteed; even a lowly SV of 1 will produce a critical result 5% of the time. Note also the impact of a high SV has, even against attacks rolling multiple dice. The effect of multiple attacks has a diminishing return on the overall probability of success (although the benefit of potentially getting multiple successes cannot be ignored). For example look at how the probability of success for a SV 12 vs SV 12 attack changes as the number of attacks increase; 40%, 60%, 71%, 77%. For that particular scenario doubling the number of dice rolled has the same impact on probability of any success as a +4 MOD.

We can also see the effect when both sides roll multiple dice; the resulting chart below is very balanced, even when compared to a roll off of one die.

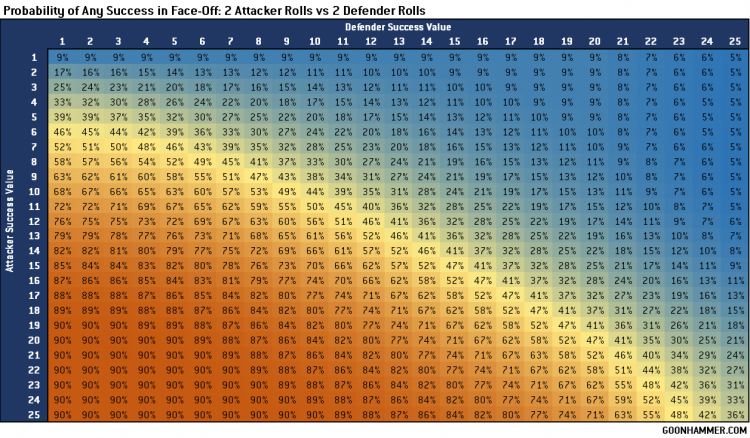
Wrapping Up

Infinity is an incredibly rewarding and deep game, and we’ve just scratched the surface of the complexity. Hopefully these charts will provide some useful insight into how probability is distributed across the spectrum of relative Success Values, and the impact of modifiers relative to the number of dice rolled. I look forward to putting together more articles like this in the future, and if you want to see anything in particular please submit your ideas here.

Thanks for reading! If you have any feedback, feel free to drop a note in the comments below or email us at contact@goonhammer.com