This week’s Hammer of Math takes a more anthropomorphically fantastical direction and looks at the dice mechanics behind Oathsworn Miniatures’ Burrows and Badgers.
Believe it or not there are games other than Warhammer 40k out there, and every now and then it’s fun to take a look at them. In this case we’re looking at Oathsworn Miniature’s Burrows and Badgers, a skirmish game featuring anthropomorphic combatants that get to sling spells, shoot arrows, and stab each other. Fancy the idea of a dual-wielding squirrel or a rabbit casually wielding a sword in plate armor? This is the game for you.

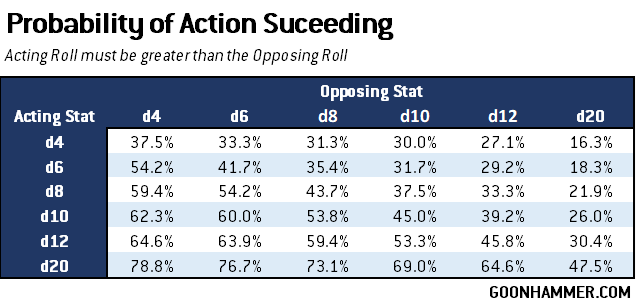
The core mechanic of Burrows and Badgers is a roll-off system where the attacking and defending models roll their respective stat dice. For melee attacks, Strike is offset against Block, while for ranged attacks the appropriately named Range is set against Nimbleness. Stats are die based and can have a d4, d6, d8, d10, d12, or d20. In order for an Action to succeed the acting player’s Roll has to be greater than the opposing Roll; ties are considered failures. Where things get interesting is the perfect roll mechanic; when a die roll hits the maximum you add 7 to the result. So a d4 roll of 4 becomes 11.
The perfect roll mechanic adds an interesting wrinkle to the probability curves, as dice with fewer faces have a higher probability of achieving a perfect roll. A d4 will get a 1, 2, or 3 75% of the time, but the remaining 25% of the time that result is an 11 and will beat anything outside of a perfect roll from a d6 through a d10. The chart below shows the resulting probabilities.
The effect of the perfect roll mechanic is that the floor and ceiling are heavily modified. Without modifiers, even the best stat has a 21.2% chance of failing against the worst stat while the worst stat still has a 16.3% chance of succeeding against the best stat. This is roughly equivalent to a d6 roll where a 1 always fails and a 6 always succeeds. The nuance comes from the comparisons in between the individual stat dice. With the exception of going from a d12 to a d20, the highest improvement in probability occurs when an acting stat can be improved across the threshold where it exceeds the opposing stat. In other words if your opponent is rolling a d8, the highest incremental improvement occurs when you raise the acting stat from a d8 to a d10. The second highest incremental improvement comes when raise the acting stat to tie the opposing stat (in the previous example, going from a d6 to a d8).

The influence of modifiers is also significant, and is unsurprisingly skewed towards lower stat values. A -1 modifier on a stat value of d4 will cap the probability of success at 25% against most rolls, and a -3 modifier (a fighter with 4 wounds or less) will cap a d6 roll at 16.7% (1 in 6). The added resiliency against modifiers is another reason why improving stats is so useful.
So to summarize:
- Assuming no modifiers, a roll-off has a roughly 1-in-6 chance of always succeeding and always failing regardless of the relative stat values.
- Improving the acting stat so that it is higher than the opposing stat produces the greatest improvement in probability of success; beyond that the demands are diminishing.
- The second greatest improvement in probability is achieved by raising the acting stat so that is equal to the opposing stat.
- Improving the acting stat significantly reduces the influence of modifiers, especially at higher die values.
Thanks for reading! If you have any questions or comments feel free to drop us a note in the Comments below or email us at contact@goonhammer.com. That’s also the best way to suggest topics for future articles.



You must be logged in to post a comment.