Hammer of Math: Expected Damage vs Expected Kills

This week’s Hammer of Math takes a look at what happens when you examine the impact of the target’s Wound characteristic when calculating how many expected damage are dealt by a particular attack.

Expected Damage

The concept of expected value is one that’s used frequently in this series; it’s a helpful tool to determine what the average number of wounds that a given attack will deal to a given target. The formula for Expected Damage (ED) is the product of all of the probabilities of success for the gatekeeping rolls (hit, wound, save, ignore wounds) and the mean values of the two driving rolls (damage and number of attacks). The formula is below:

Expected Damage = Shots x Damage x P(Hit) x P(Wound) x [1 – P(Save)] x [1 – P(IW)]

The result is a fairly simple calculation that’s quicker than running simulations or using a web program like the Warhammer Stats Engine courtesy of /u/Uily on Reddit. For example a Space Marine (BS 3+) firing a lascannon (S9, AP -3, D1d6) at a Carnifex (T7, 3+, 8W) will result in the equation below. The 3.5 damage comes from the average value of a d6, which is the sum of all possible outcomes divided by the number of possible outcomes. In the case of a d6 the outcomes are 1, 2, 3, 4, 5, and 6 for a sum of 21 and the number of outcomes is 6, leaving us with 3.5 as the average.

1 Shot x 3.5 Damage x 0.66 P(Hit) x 0.66 P(Wound) x [1 – 0.17 P(Save)] x [1 – 0 P(IW)] = 1.30 Wounds

Normally one would take this calculation, divide the number of wounds the Carnifex has, and use that to calculate the average number of shots required to kill the target. Since the Carnifex has 8 wounds on average the lascannon should require an average of 6.2 shots to kill it. This approach works best for situations where the damage inflicted by the attack is less than the number of wounds of the target. But what happens if the target is an Aggressor instead of a Carnifex? The expected value is the same, but will it take an average of 2.3 shots to kill an Aggressor? It won’t. In reality the required number of shots is higher, because ED calculations fail to take into account that damage dealt in excess of the Wounds characteristic of the target is lost.

Effective Mean Damage and Expected Kills

In order to accommodate this discrepancy the calculation needs to take into account the Wounds characteristic of the target. There are multiple ways to do this, such as looking at damage dealt in terms of the ratio of number of shots required to kill the target, but I have found the most intuitive to be to cap off the damage dealt by the weapon so that values in excess of the Wounds characteristic of the target equal the characteristic. In the case of the Aggressor any damage result in excess of 3 is effectively 3 damage, so if we look at the lascannon any d6 results above 3 will count as three. The resulting effective mean damage is (1 + 2 + 3 + 3+ 3+ 3) / 6 = 2.5, which is a full point of damage less than the average outcome of a d6. The chart below shows the effective mean for d6 and d3 damage weapons against different Wound characteristics.

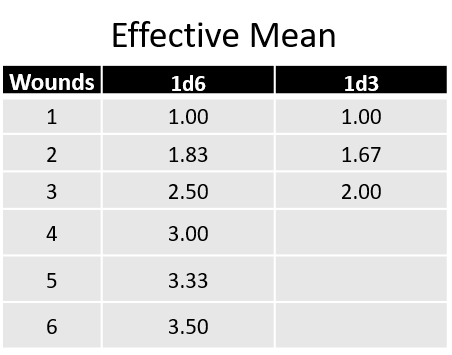
If we apply this effective mean to the expected damage formula and divide the number wounds of the target by the result, we get the Expected Kills (EK) per attack.

Expected Kills = Target Wounds / (Shots x Effective Mean Damage x P(Hit) x P(Wound) x [1 – P(Save)] x [1 – P(IW)])

In the case of the Carnifex being shot at by the Space Marine wielding a lascannon the EK is the same as dividing the Expected Damage by 8 wounds for a value of 6.2 attacks. For the Aggressor the resulting EK is 3.2, which is higher than the 2.3 shots we got from using the uncorrected ED results. To validate this approach I ran simulations against three targets with similar probability profiles (same toughness, same save) but different wound values. The resulting chart is below.

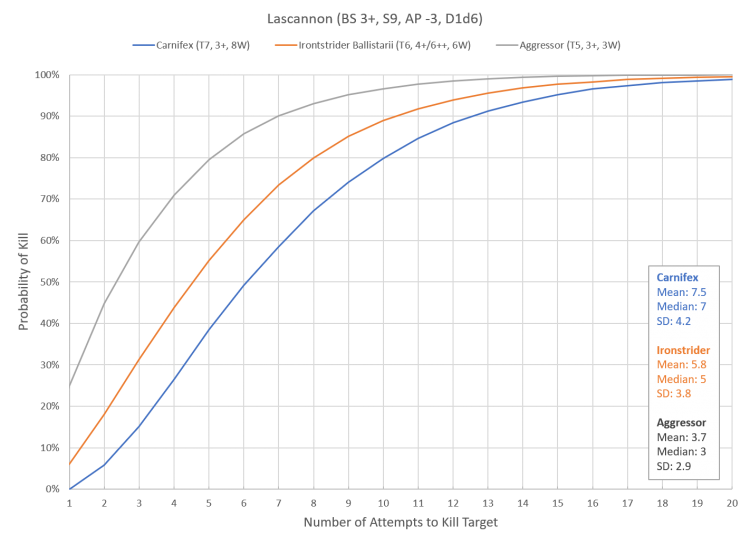
The calculations from the EK equation estimated an average of 6.2 attacks to kill the Carnifex, 4.7 shots to kill the Ironstrider Ballstrarii, and 3.4 attacks to kill the Aggressor. The actual mean number of attacks required to kill the target is consistently higher than the calculated values. Originally I was concerned that the issue might be a function of small sample size, but after boosting the iteration to 100,000 shots the results are consistent. My best guess is that the disparity between the calculations and the simulations is due to the fact that the calculations fail to take into account the sequential nature of rolls in 40K, meaning that more damage is ‘wasted’ if a high damage shot occurs after the target is reduced to a single wound from a previous attack. To accommodate this discrepancy and producing a conservative estimate I suggest taking the expected kills calculation and rounding up.

Wrapping Up

By slightly tweaking the Expected Damage calculations we can achieve a more relevant value that more accurately indicates the effectiveness of an attack against a given target. The steps below summarize the approach.

1. Calculate the effective mean damage.
2. Use the effective mean damage to calculate the Expected Damage.
3. Divide the number of wounds by the calculated Expected Damage to get the number of Expected Kills.
4. Round up to the nearest whole number.

The end result is a conservative estimate of the average number of attacks that will produce an above average chance of killing the target.

Thanks for reading! If you have any feedback, feel free to drop a note in the comments below or email us at contact@goonhammer.com. If you have any questions that you would like answered in a future article, please submit them here.