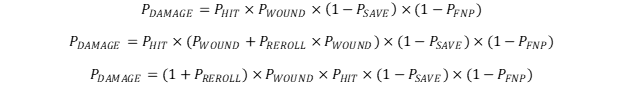There’s a lot of randomness in Warhammer. Understanding that randomness and how to predict outcomes is a powerful tool in a general’s arsenal. In Hammer of Math, we dive into probability and statistics to do just that, tackling specific topics in Warhammer. This week, Kevin Genson is doing an analysis of modifiers and re-rolls, and how they affect outcomes.
Back in April TheChirurgeon posted a helpful article on the basics of probability as it relates to Warhammer 40,000. In it he discussed the fundamental rules of probability, the nature of independent events, and the concepts of expected value and variance. These tools can be very helpful when examining the effectiveness of various options against targets. In this article we’re going to take a deeper dive into how probability is influenced by re-rolls, and what you can do to maximize your chances of success.
The Fundamental Rolls and Expected Damage
Every attack in Warhammer 40,000 is dependent on the interaction of a series of probabilistic events. The most common attack sequence is a function of four statistically independent events (assuming a fixed damage and number of shots). Remember that in Statistics two events are independent if their probabilities do not affect each other, so in Warhammer independent events are die rolls that are not affected by other die rolls.
- The hit roll
- The wound roll
- The save roll
- The Feel No Pain roll
In order for an attack to succeed, those four rolls have to go the player’s way. It’s important to understand that because these rolls are independent their order does not matter for the purposes of determining probabilities. The outcome of the hit roll, for example, does not affect the outcome of the wound roll in any way. Outside of special rules like the Primaris Infiltrator’s Marksman bolt carbine automatically wounding on a hit roll of 6, there is no interference between the events. The probability equation for this is below:
There are two additional rolls that need to be considered; the shots roll (the number of shots an attack performs) and the damage roll. Although these events are independent in the sense that their probability is not connected to any other events, they heavily determine the outcome of the attack by determining the quantity of wounds dealt. For the sake of clarity I’ve called these events driving rolls while the other rolls that only influence probability are gatekeeping rolls. Driving rolls determine the quantity of the attack, gatekeeping rolls determine how successful the attack is. Together this gives you the final estimate for damage:
In other words the expected level of damage is the product of the shots roll, the damage roll, and probability of damage. It’s a quick and easy way to estimate how much damage a given attack is expected to make, but it leaves one thing out; the distribution of outcomes. Expected damage gives you the average result, but it does not tell you how likely that is to occur. Nor does it tell you how much the result could vary. In order to perfectly understand the distribution of outcomes you would need to calculate every possible permutation of die rolls. This can easily be thousands or hundreds of thousands of combinations. The math sucks.
So let’s be lazy instead.
Simulations and Probability Distribution
Rather than try to perfectly understand the distribution of probability, I exploited the fact that I’m lazy and that perfects results don’t matter to create a fairly simple program that simulates a few thousand rolls and gives you the final outcome.
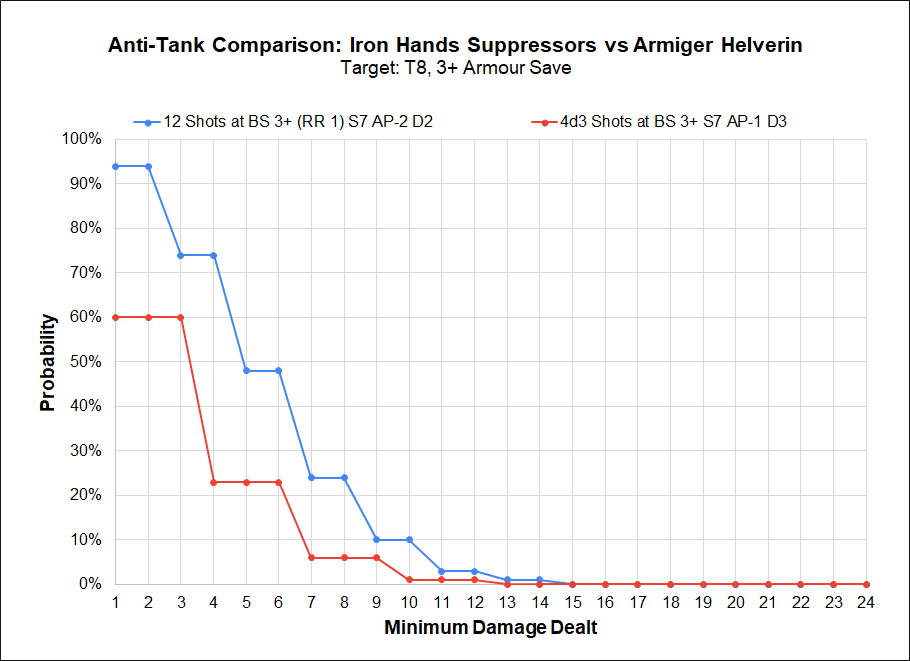
What this lets us do is examine the distribution of possible outcomes for a given scenario. You input the result needed for a successful hit, wound, save, and FNP (“Feel No Pain,” abilities that allow you to ignore damage such as the Death Guard’s Disgustingly Resilient) along with the damage and number of shots and the spreadsheet does the rest. For example, the image below compares the outcome of six Iron Hands Suppressors to an Armiger Helverin against a T8 target with a 3+ armor save.
The expected damage for 6 IH Suppressors is 5.2 wounds when you include the ability to reroll 1s. For the undamaged Armiger Helverin the expected damage is 1.8 wounds. What those values don’t tell you is the distribution of results. The Helverin is expected to do no damage 40% of the time, while only 6% of the attacks by the Suppressors will do no damage. This is why the distribution of outcomes is so important.
Gatekeeping Rolls
The hit, wound, save, and FNP rolls all serve the same purpose; reducing the probability of success. Probability can only be decreased, and because a roll of 1 always fails we have a “baseline” probability that can never be improved. Assuming “perfect” conditions of a 2+ to hit, 2+ to wound, and no save or FNP, the highest probability that an unmodified attack has to wound is 69%. Nice.
The Influence of Rerolls on Gatekeeping Rolls
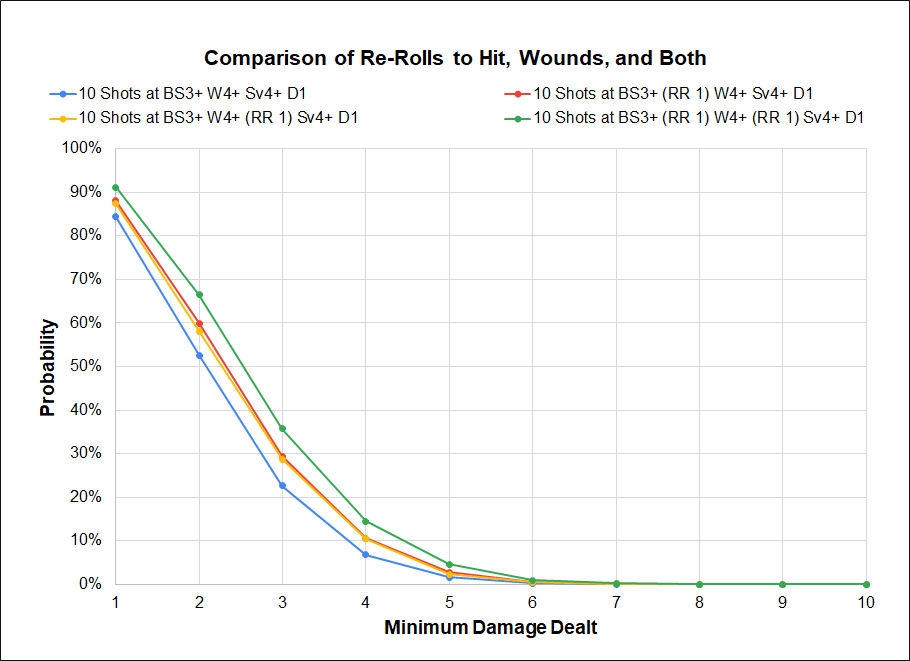
Regardless of the roll, re-rolls provide a fixed alteration to the probability in the form of a 16.7% (1/6) increase for every number that is re-rolled. So re-rolling 1s gives a 16.7% boost, re-rolling 1s and 2s provides a 33% improvement, etc. In other words the influence of a Primaris Captain (re-roll 1s to hit) and Primaris Lieutenant (re-roll 1s to wound) are identical. The effect of modifying different rolls is multiplicative; re-rolling 1s on hit and wounds is a 36% improvement (1.167*1.167). The proof is below, and it’s also demonstrated in the simulation.
The blue line is our baseline of 5 Primaris rapid firing at Chaos Space Marines: 10 shots hitting on a 3+, wounding on a 4+, and the target getting a 4+ save. The expected damage for 10 shots at BS 3+, 4+ to wound, and a 4+ save is 1.67. Rerolling a 1 on the hit or wound roll increases the expected value to 1.94, and rerolling both increases the expected value to 2.27. This is greater than the expected value from rerolling misses (hit rolls of 1 or 2), which is 2.22. As you can see, stacking rerolls can be very effective.
The Influence of Modifiers on Gatekeeping Rolls
The impact of a modifier depends on the initial probability of the roll being modified. Unlike re-rolls, modifiers are not static. Their influence is greater when the probability of success is already low, and the magnitude of the influence is the same regardless of whether the modifier is positive or negative. The table below shows the impact of a positive and negative modifier on probability.
| Roll | Initial Probability | -1 Modifier Probability | Delta | +1 Modifier Probability | Delta |
| 2+ | 83% | 67% | -20% | 83% | +0% |
| 3+ | 67% | 50% | -25% | 83% | +25% |
| 4+ | 50% | 33% | -33% | 67% | +33% |
| 5+ | 33% | 17% | -50% | 50% | +50% |
| 6+ | 17% | 0% | -100% | 33% | +100% |
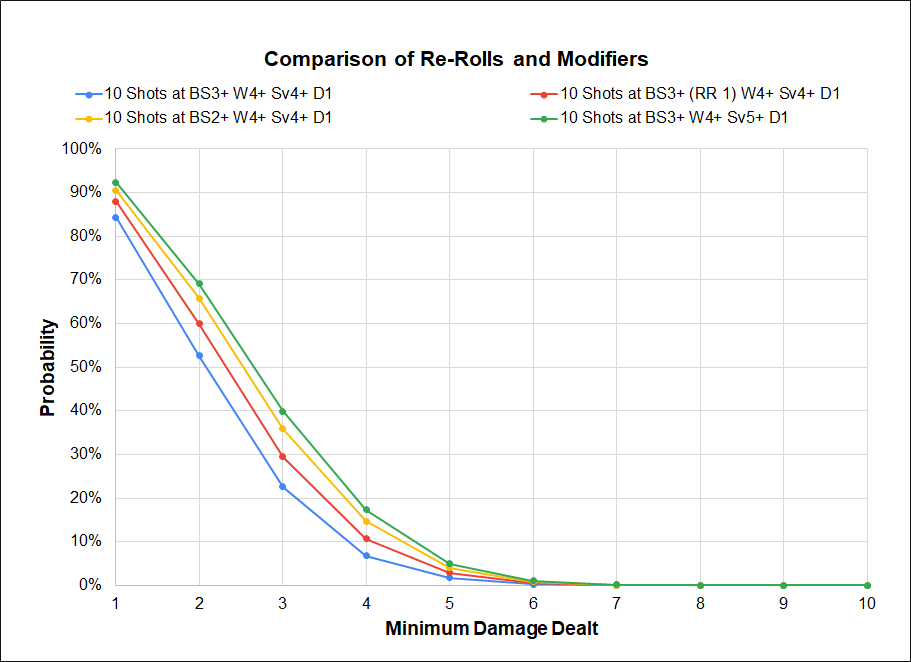
Remember that the bonus from rerolls is a flat 16.7% improvement, which means that modifiers are always going to have a greater impact on probability than rerolling a single number. Armor save modifiers are by far the most common modifier seen in the game, and since most models have at least a 6+ save the difference between AP 0 and AP -1 is significant. This can be seen in the chart below.
The blue line is once again our baseline Primaris rapid firing on Heretic Astartes; 10 shots hitting on a 3+, wounding on a 4+, and the target getting a 4+ save. We compare the influence of a Primaris Captain aura (re-roll 1s), getting a +1 to hit, and improving the AP by -1 through the tactical doctrine. The reduction in AP provides the greatest increase in probability, followed by the improvement to BS, and then finally the re-roll.
Major Takeaways
- Gatekeeping rolls only influence probability, and outside of special circumstances each roll does not influence the others.
- The impact of rerolling a fixed number is a flat 16.7% increase in probability per number; rerolling 1s or 2s would improve your chance of success by 33%.
- The effect of rerolls is multiplicative between rolls; rerolling 1s on the hit and wound roll has a cumulative improvement of 36%.
- The effect of a modifier is inversely proportional to the probability of the roll; the worse your chances of success, the greater the impact of a modifier to that roll.
- Outside of edge cases where probability cannot be changed, modifiers have a greater impact on probability than rerolls.
Driving Rolls
In contrast to gatekeeping rolls, driving rolls directly influence the final outcome by determining either the number of wounds, or the number of attacks, that are dealt to the target. From a mathematical perspective both driving rolls have an equal influence on the total wounds dealt to the target. In other words the total damage dealt to a target will be the same if you double the number or shots or double the damage. From a game perspective the inherent inefficiencies with excess wounds and the limited options for rerolling generally encourage modifying the number of shots over the damage. This is particularly true when considering the use of a Command Re-roll Stratagem; because you can only use it once per phase you’re better off applying it to the number of shots.
The Influence of Re-rolls on Driving Rolls
Because driving rolls produce a quantitative result (number of shots) instead of a binary result (pass/fail) some additional strategy is required when considering when to use a re-roll. The most important thing is to consider the expected value of the die being re-rolled; from a mathematical perspective you should only use a re-roll when the die value is less than the expected value. For a d3 this value is 2, and for a d6 this value is 3.5.
| Re-Roll Target | Probability of Poor Result | Probability of Even Result | Probability of Good Result | Expected Value w/ RR | Delta |
| 1 | 0% | 17% | 83% | 3.92 | +12% |
| 2 | 17% | 17% | 67% | 4.17 | +19% |
| 3 | 33% | 17% | 50% | 4.25 | +21% |
| 4 | 50% | 17% | 33% | 4.17 | +19% |
| 5 | 67% | 17% | 17% | 3.92 | +12% |
| 6 | What are you doing. No. Don’t re-roll the best option. | ||||
From the chart above we see that the highest improvement to probability comes from re-rolling a d6 when the result is less than or equal to 3. A more conservative player may prefer to only re-roll values of 1 or 2 for a slightly reduced improvement with the benefit of cutting the chances of a negative result in half.
The presence of any re-roll at all does significantly influence the probability of doing damage, and as expected re-rolling results of 3 or worse on a d6 provides the greatest benefit. Compared to the benefit of having any reroll at all the improvement between re-rolling 1s, 2s, or 3s is relatively minor.
The Influence of Modifiers on Driving Rolls
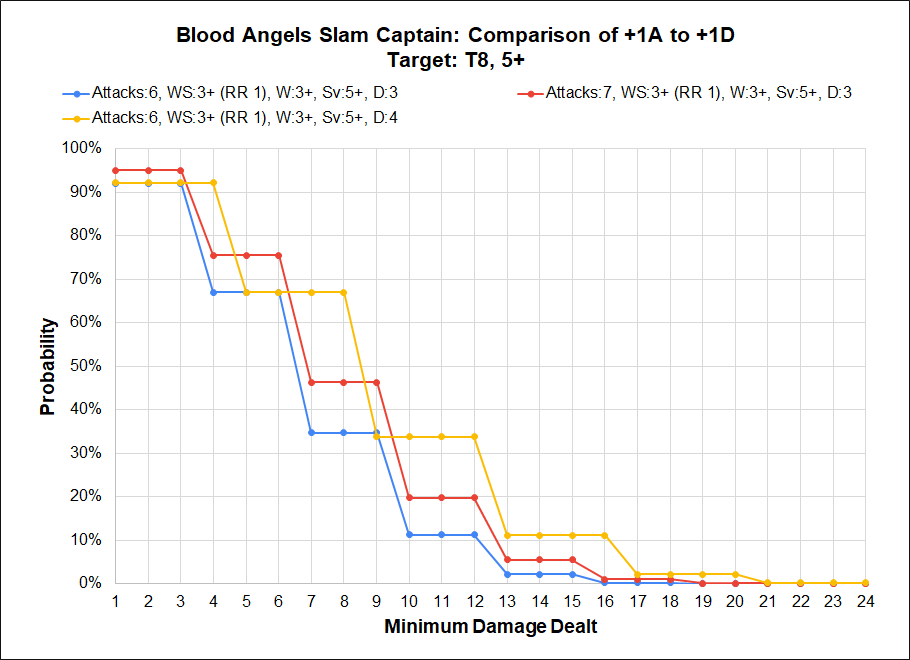
The influence of modifiers is fairly simple; it’s a flat increase proportional to the roll being made. For example adding 1 damage to a 1d3 weapon is a 50% increase (the expected value of 1d3 is 2, dividing 3 by 2 is 150%). The most important thing to remember is that the effect of an additive modifiers (+1 attacks, +1 damage) is reduced as the number being modified gets larger. In contrast multiplicative effects (double attacks, half damage) affect the outcome the same regardless of the number being modified. We can verify this by comparing the expected value of 5 Intercessors rapid firing auto bolt rifles in the Tactical Doctrine to 5 Intercessors firing Stalker Bolt rifles in the same phase. Remember that expected damage is the product of the number of shots, damage, and probability of damage.
In this scenario the probability of damage is the same, and either the shots or damage are doubled. Therefore the expected value is the same. We can chart the results to see what the distribution looks like below. The minimum damage distribution of the doubled damage and doubled shots roughly overlap; with the double damage line naturally having a series of 2-damage steps.
Major Takeaways
-
- Driving rolls significantly impact the outcome of a particular attack; in general it is preferable to re-roll the number of shots over a particular gatekeeping roll.
- The most advantageous re-roll is when the result of a driving roll is less than the expected value, although the possibility of getting a negative result means that it may not be worthwhile to re-roll a value higher than one.
- The effect of an additive modifier (such as a +1 damage effect) on a driving roll or value (such as fixed damage) is highest when the value being modified is low.
- Multiplicative effects will influence probability equally when applied to damage or the number of shots, regardless of the original value. Bear in mind that in 40k, excess damage is wasted, so this won’t always be true in practice – for example, all other things being equal, a 10 shot 2 damage gun is mathematically identical to a 5 shot 4 damage gun, but if the models in the target unit have 2 or fewer wounds you’ll get higher performance out of the 10 shots than the 5 shots.
Conclusions
Math is the foundation of Warhammer 40K, and by understanding some of the principles of probability you can potentially squeeze out every last bit of potential out of your army. It may seem like a small difference between choosing +1 attack or +1 damage to a weapon, but due to the nature of the game the results can be significant. As always, if you have any questions, comments, or things you’d like to add, feel free to drop us a message in the comments section below, or shoot us an email at contact@goonhammer.com.