This week’s Hammer of Math takes a look at the narrative side of 40K and examines some of the numbers behind the Crusade system and getting your Astartes interred in a Dreadnought as quickly as possible.

I’ll freely admit; as much as I love to crunch numbers and talk about competitive play I’m a narrative player at heart. Part of it is because I’m inexcusably terrible at playing the game, but the other part is that I’ve been a fan of 40K since the mid-90s and the lore has always stuck with me even when the game itself waxes and wanes. The Crusade system is particularly appealing because it allows a player to literally forge a narrative out of gameplay and excitement. For example in a local Crusade campaign that I’m involved in a squad of Servitors inexplicably managed to beat a Lord of Contagion to death (that the Lord of Contagion had already been worn down by the combined efforts of a Gravis Captain and an Aggressor squad is irrelevant). As such they were renamed from “Salvage Unit Alpha” to “SAVAGE UNIT ALPHA” (the capitalization is critical) and earned enough XP to gain the Headhunters trait and get a +1 to hit and wound CHARACTERS. They have subsequently died in every mission, as is their lot, but they remain the Servitor equivalent of heroes.
One thing that will never happen to SAVAGE UNIT ALPHA is the glory of being upgraded to a walking box of death incarnate. When Games Workshop did their Codex show one of the things they revealed was that a sufficiently injured Space Marine CHARACTER could be interred as a Dreadnought with all of the experience of the previous unit. In order to do this our Hero must gain two Battle Scars, which is surprisingly difficult as it requires a result of 1 on the d6 Out of Action roll made after a unit is destroyed in a battle. Extraordinarily (un)lucky Heros have a 2.7% chance of getting two Battle Scars after falling in two battles, but how many times must our Hero die to have a better than average chance of being put into a box with legs?

The way to solve this problem is to think about in terms of possible outcomes over the course of the Hero’s career. Ultimately we care about three scenarios:
- The Hero never receives a Battle Scar, meaning they never roll a 1 on any dice. This is P(X = 0).
- The Hero receives only 1 Battle Scar, meaning they roll 1 once and then never roll it again. This is P(X = 1).
- The Hero receives two or more Battle Scars, meaning they roll a 1 at least two times and are eligible for internment. This is P(X ≥ 2).
These outcomes are complementary events, meaning that if one happens the other cannot and the probability that one of them will happen is 1. But given N possible deaths, how can we determine what the probabilities are?
For P(X=0) the answer is simple; every die roll must hit the 5/6 chance that a 1 doesn’t appear. The cumulative probability of an outcome over N is the product of the N individual probabilities:
P(X=0) = (5/6)^N
Things are a little more tricky for getting a single 1. For this we have to look at binomial probability, which is the probability that exactly X successes on N repeated trials will occur. It only works for events which have two outcomes (success or fail) and a fixed probability P. In our case the probability of getting a 1 (what we call a “success” although the Hero may disagree) is 1/6. The equation requires you to first establish the number of possible combinations (X results picked out of N trials) and then multiply that by the probability of X successes and the probability of (N-X) failures. The exclamation point indicates a factorial.
P (X = N) = [N!/X!(N-X)!] * P^X * (1 – P)^(N-X)
If you set X to 0 then the equation simplifies to the probability of P(X=0). For the second case X is 1, which means the number of possible combinations simplifies down to N. The rest of the equation simplifies to:
P(X = 1) = N * (1/6) * (5/6)^(N-1)
Since the three outcomes are complementary and we know the probability of the first two outcomes we can calculate the probability of the third.
P (X ≥ 2) = 1 – P(X=0) – P(X=1) = 1 – (5/6)^N – N * (1/6) * (5/6)^(N-1)
Which is pretty easy to graph. The line we’re looking for is the gray one; the orange and blue were kept for convenience.
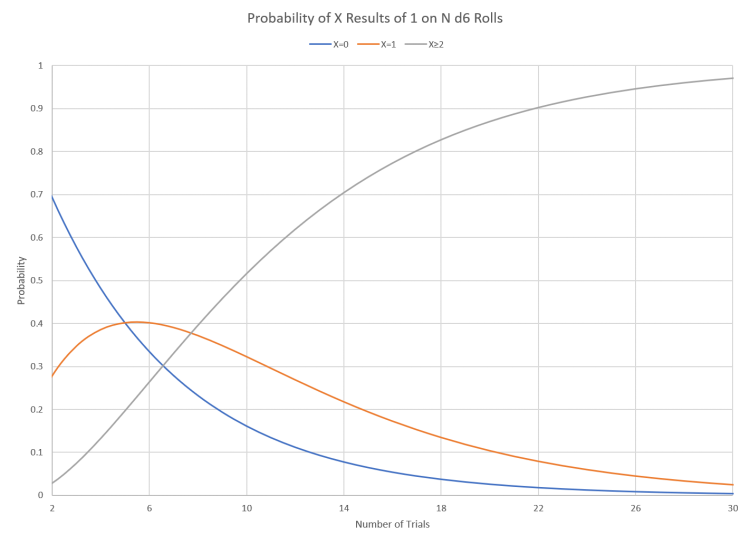
So the answer to our question is that a Space Marine needs to be destroyed around ten times to have a better than average chance of being eligible to be interred in a dreadnought. Of course this is a distribution; 3% of the Crusaders will be destroyed thirty times without obtaining enough Battle Scars to qualify.
Lucky them.



You must be logged in to post a comment.