This week’s Hammer of Math answers a question that Bair has been wondering about Horus Heresy: how many lascannons does it take to get to the Space Marine center of a Land Raider?
Back in July I did an article on the basics of Horus Heresy, which included a brief discussion on how killing vehicles works. Last week our resident Heresy aficionado (heretic?) Bair asked me about what it would take to kill a Land Raider using the marquee anti-tank weapon; the lascannon. Largely relegated to a joke in 9th 40k due to the combination of fairly mediocre strength, low AP, and highly variable damage, this weapon is significantly nastier in Horus Heresy. The reason for this is pretty simple: the stats are just better.
- The lascannon has a Strength characteristic of 9, which means it has a chance to penetrate any armour (which caps out at 14).
- The Armour Penetration characteristic of 2 gives a +1 on the Vehicle Damage table, which allows it to have a 1 in 6 chance of blowing up the target on any Penetrating hit.
- It allows you to re-roll the test against the target’s Armour Value.
So with that in mind let’s take a look at what it takes to kill the iconic Land Raider, which is the ultimate Metal Box. The work of the famous techno-archaeologist Arkhan Land who discovered the STC template for what would ultimately become the Land Raider, it features a combination of tough armor, heavy firepower, and the capacity to carry a full squad of Astartes. Against nearly any foe this is a terrifying threat. In the Horus Heresy this is characterized by an Armour Value of 14, 5 Hull Points, and it can an Evasion Reaction to gain Shrouded which provides an effective 5+ save against Glancing or Penetrating hits.
The Math
We can solve this problem directly using binomial probability, a technique that I have discussed previously in numerous articles. In short this is the probability that a given number of successes will occur over a given number of trials for a fixed probability. This can be expanded to cumulative probability, which is the likelihood that up to a given number of successes will occur. In Horus Heresy there are two binomial probabilities we’re interested in.
- The probability that at least 5 results that remove a Hull Point will will occur over the given number of attacks, or more specifically the one minus the cumulative binomial probability that up to 4 successes will occur.
- The probability that at least 1 results will cause a Penetrating Hit that explodes (rolling a 6 on the Armour Penetration Roll followed by a 6 on the Vehicle Damage Table). This is translated to 1 minus the probability that none of the attacks will be a success.
By adding these two probabilities together you get the likelihood that the attacks will destroy the target.
The Complications
Of course nothing Games Workshop writes is ever simple, and in the case of this scenario there are two complicating factors. The first complicating factor is if the Land Raider makes an Evasion Reaction, which would mean that 33% of the time every Glancing or Penetrating Hit is discarded. Second, there’s the influence of re-rolling the Armour Penetration Roll. You can either re-roll any attack that doesn’t produce a Glancing or Penetrating Hit, or if you’re fishing for an explosion you can re-roll everything that isn’t a Penetrating Hit. The influence of modifiers and re-rolls is the first article I wrote for this column, and fortunately the math hasn’t changed since then. The influence of a re-rolling is additive; you take the original probability of success and multiply that by the probability of re-rolling and the original probability of success. Between the two effects we’re dealing with four possible scenarios assuming a hit, which means four probabilities.
- Re-rolling Armour Penetration Roll results of 1 to 4 against a non-evading target. The chance of taking off a Hull Point is 56% and the chance of a single hit killing the target is 4.6%.
- The same scenario above against an evading target reduces the probabilities to 37% and 3.1% respectively.
- Re-rolling results of 1-5 when the target doesn’t evade has a 44.4% chance of taking off a Hull Point and 5.1% chance of getting two sixes.
- If the target is evading when you re-roll results of 1-5 the chances change to 37.0% and 3.1%.
The final wrinkles are the number of attackers and the effective BS for the hit roll. Combine all of these probabilities and you get a series of results that’s best displayed in a chart.
The Charts
I’ve crunched the numbers and put them into two charts. The first is when the Land Raider is not evading, and the second for when it does. To use it you cross-reference the number of lascannons firing with the effective BS of the attack. Comparing re-rolling 1-4 vs 1-5 shows that there is a threshold under which it is optimal to re-roll any Armour Penetration Roll that isn’t a Penetrating Hit versus only rolling results that have no effect. What’s notable is that a 6+ to hit (such as a Reaction shot) is where it’s always optimal to re-roll any result regardless of the number of attacks, and for a BS of 3+ that scenario is any time where the attack has 5 or fewer models.
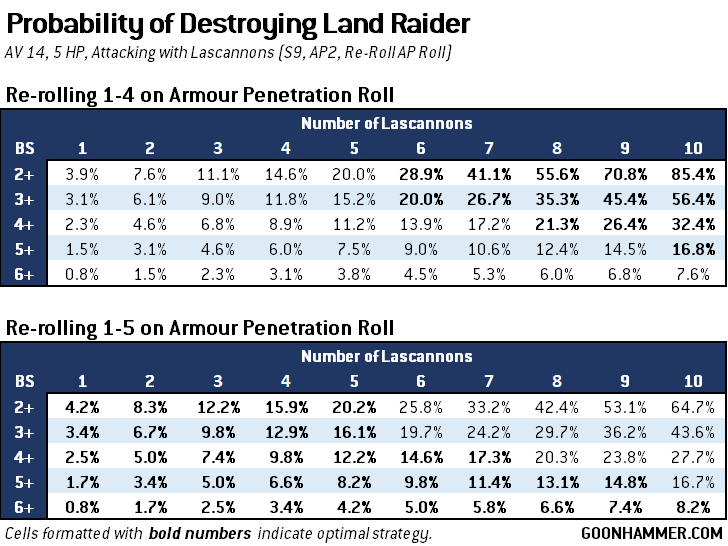The optimal approach shifts slightly when the target has the ability to ignore damage on a 5+. In that case the optimal strategy line shifts to the right to include any groups of six or fewer, and in the case of a BS 3+ unit the optimal strategy against an evading Land Raider is to re-roll glances for units of up to 7 models.
This makes sense when you consider the difference between achieving a kill through hull points or a penetrating hit. While the probability of removing an individual hull point is always higher than the probability of getting two sixes in a row, you still have to achieve at least five successes. The cumulative probability of that happening decreases precipitously as the chances of an individual success go down, to the point where you’re more likely to achieve a penetrating hit and therefore it’s in your best interest to maximize that.
Wrapping Up
Killing vehicles in Horus Heresy is an interesting blend of steady degradation combined with a small chance of achieving a killing blow. The lascannon’s ability to re-roll Armour Penetration Rolls makes it a fun challenge to explore and provides an example of how to use binomial probability to determine the optimal strategy. We quickly see that as the number of attacks or the probability of hitting decreases the optimal strategy shifts from re-rolling null results to re-rolling any result that doesn’t provide a chance to penetrate and kill the target. Hopefully this proves useful to you on the battlefield, and as always thanks for reading!
If you have any questions or comments feel free to drop us a note in the Comments below or email us at contact@goonhammer.com. That’s also the best way to suggest topics for future articles.
